鳶尾花數據集#
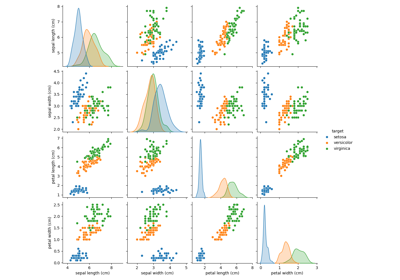
此數據集包含三種不同鳶尾花(山鳶尾、變色鳶尾和維吉尼亞鳶尾)的花瓣和萼片長度,存儲在一個 150x4 的 numpy.ndarray 中
行代表樣本,列代表:萼片長度、萼片寬度、花瓣長度和花瓣寬度。
下圖使用了前兩個特徵。有關此數據集的更多信息,請參閱這裡。
# Code source: Gaël Varoquaux
# Modified for documentation by Jaques Grobler
# License: BSD 3 clause
載入鳶尾花數據集#
from sklearn import datasets
iris = datasets.load_iris()
鳶尾花數據集的散點圖#
import matplotlib.pyplot as plt
_, ax = plt.subplots()
scatter = ax.scatter(iris.data[:, 0], iris.data[:, 1], c=iris.target)
ax.set(xlabel=iris.feature_names[0], ylabel=iris.feature_names[1])
_ = ax.legend(
scatter.legend_elements()[0], iris.target_names, loc="lower right", title="Classes"
)
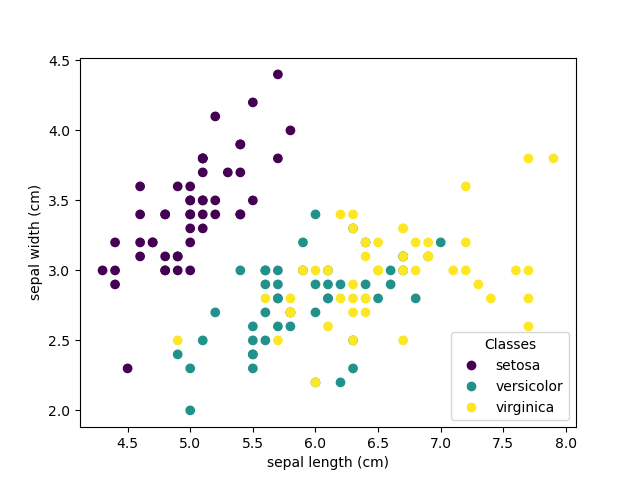
散點圖中的每個點都代表數據集中 150 朵鳶尾花中的一朵,顏色表示它們各自的類型(山鳶尾、變色鳶尾和維吉尼亞鳶尾)。您已經可以看到有關山鳶尾類型的模式,可以根據其短而寬的萼片輕鬆識別。僅考慮這兩個維度,即萼片寬度和長度,變色鳶尾和維吉尼亞鳶尾類型之間仍然存在重疊。
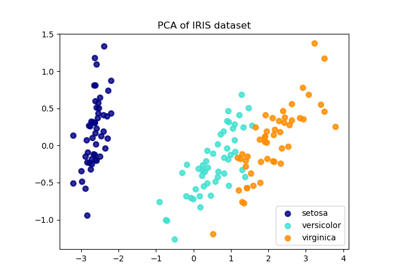
繪製 PCA 表示#
讓我們將主成分分析 (PCA) 應用於鳶尾花數據集,然後在前三個 PCA 維度上繪製鳶尾花。這將使我們能夠更好地區分這三種類型!
# unused but required import for doing 3d projections with matplotlib < 3.2
import mpl_toolkits.mplot3d # noqa: F401
from sklearn.decomposition import PCA
fig = plt.figure(1, figsize=(8, 6))
ax = fig.add_subplot(111, projection="3d", elev=-150, azim=110)
X_reduced = PCA(n_components=3).fit_transform(iris.data)
ax.scatter(
X_reduced[:, 0],
X_reduced[:, 1],
X_reduced[:, 2],
c=iris.target,
s=40,
)
ax.set_title("First three PCA dimensions")
ax.set_xlabel("1st Eigenvector")
ax.xaxis.set_ticklabels([])
ax.set_ylabel("2nd Eigenvector")
ax.yaxis.set_ticklabels([])
ax.set_zlabel("3rd Eigenvector")
ax.zaxis.set_ticklabels([])
plt.show()
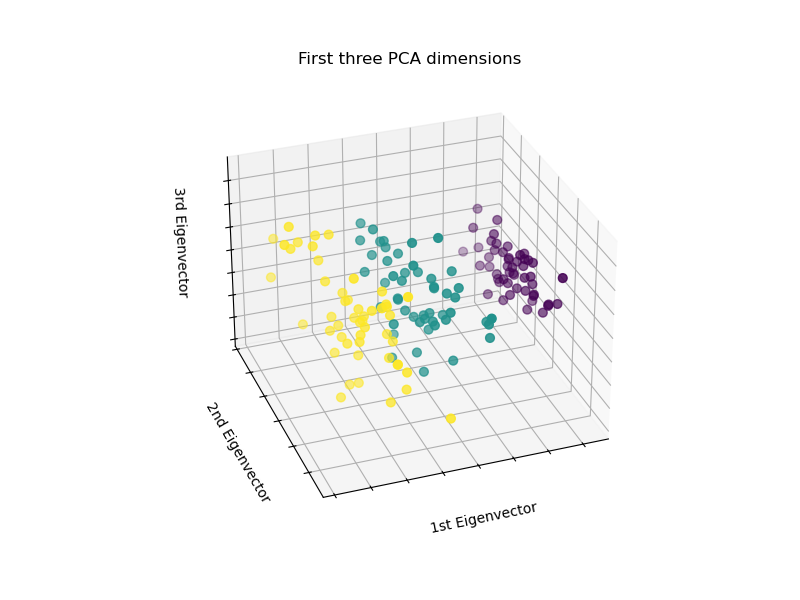
PCA 將創建 3 個新特徵,它們是 4 個原始特徵的線性組合。此外,這種轉換最大化了方差。通過這種轉換,我們看到我們可以使用第一個特徵(即第一個特徵值)來識別每個物種。
腳本總運行時間:(0 分鐘 0.227 秒)
相關範例